5.3.1. Heterogeneity and inconsistency

GRADE uses inconsistency and heterogeneity rather interchangeably. However, there are some important nuances:

• A heterogeneity in effect – where it can be assumed that it is randomly distributed – may be due to random variation in the effect amongst studies. To properly address this, the pooled effect should be calculated using random modelling (RevMan uses the DerSimonian and Laird random effects model, but other techniques, such as Bayesian and maximum likelihood, are often used as well). An important condition for the use of these techniques is that it must be plausible that the heterogeneous effect is randomly distributed, which is not always easy to verify. DerSimonian, Laird and maximum likelihood methods have an additional assumption that the effect is normally distributed, while with Bayesian techniques another distribution can be used as well. The studies in this case cannot be considered as inconsistent, and the heterogeneity is accounted for here by the larger confidence interval, so no downgrading is needed here. Note that if the heterogeneity statistic Q is less than or equal to its degrees of freedom (so if I² = 0), DerSimonian gives results that are numerically identical to the (non random effects) inverse variance method.
• If heterogeneity is important for one reason or another, but all estimates point in the same direction, e.g. a strong or very strong effect of the intervention, then one should not necessary downgrade for inconsistency but make a judgement on the plausibility of the study results.

5.3.2. Judging heterogeneity and inconsistency

Exploring and judging heterogeneity is probably the most difficult part in performing and judging a meta-analysis. A number of rules are presented, but a full explanation can be found in the Cochrane Handbook (chapters 9.5 and 9.6). A KCE expert exploring and judging heterogeneity should at least have a good understanding of and ability to apply this Cochrane guidance. If not, he/she should ask for help from somebody who does.

GRADE identifies four criteria for assessing inconsistency in results, and reviewers should consider rating down for inconsistency when:

1. Point estimates vary widely across studies;
2. Confidence intervals (CIs) show minimal or no overlap;
3. The statistical test for heterogeneity which tests the null hypothesis that all studies in a meta-analysis have the same underlying magnitude of effect shows a low p-value;
4. The I², which quantifies the proportion of the variation in point estimates due to between-study differences, is large

In the past, rigid criteria were used to judge heterogeneity, e.g. an I² of 50% used to be a common threshold. This improves the consistency in judgments, but one risks to be consistently wrong. All statistical approaches have their limitations, and their results should be seen in the context of a subjective examination of the variability in point estimates and the overlap in CIs. So again, transparent judgments are essential here.

What is a large I²? One set of criteria would say that an I² of less than 40% is low, 30 to 60% may be moderate, 50 to 90% may be substantial, and 75 to 100% is considerable. Note the overlapping ranges and the equivocation (‘‘may be’’): an implicit acknowledgment that the thresholds are both arbitrary and uncertain. When individual study sample sizes are small, point estimates may vary substantially, but because variation may be explained by chance, I² may be low. Conversely, when study sample size is large, a relatively small difference in point estimates can yield a large I².

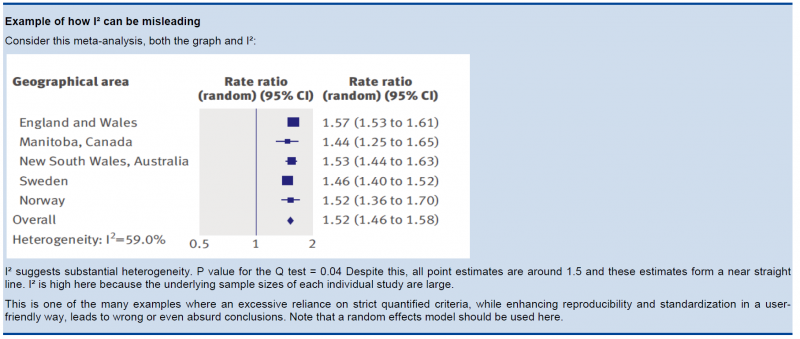
5.3.3. Other considerations

• Risk differences (i.e. absolute risk reductions) in subpopulations tend to vary widely. Relative risk (RR) reductions, on the other hand, tend to be similar across subgroups, even if subgroups have substantial differences in baseline risk. GRADE considers the issue of difference in absolute effect in subgroups of patients, much more common than differences in relative effect, as a separate issue. When easily identifiable patient characteristics confidently permit classifying patients into subpopulations at appreciably different risk, absolute differences in outcome between intervention and control groups will differ substantially between these subpopulations. This may well warrant differences in recommendations across subpopulations.
• Rate down for inconsistency, not up for consistency.
• Even when there is heterogeneity in effect, one must evaluate if the heterogeneity affects your judgment on clinical effectiveness, e.g. when there are large differences in the effect size, but when the estimations point to the same direction (all beneficial or all harmful).
• Reviewers should combine results only if – across the range of patients, interventions, and outcomes considered – it is plausible that the underlying magnitude of treatment effect is similar. This decision is a matter of judgment. Magnitude of intervention effects may differ across studies, due to the population (e.g. disease severity), the interventions (e.g. doses, co-interventions, comparison of interventions), the outcomes (e.g. duration of follow-up), or the study methods (e.g. randomized trials with higher and lower risk of bias). If one of the first three categories provides the explanation, review authors should offer different estimates across patient groups, interventions, or outcomes. Guideline panelists are then likely to offer different recommendations for different patient groups and interventions. If study methods provide a compelling explanation for differences in results between studies, then authors should consider focusing on effect estimates from studies with a lower risk of bias.

Beware of subgroup analyses. The warning below originates from the Cochrane Handbook (chapter 9.6). When confronted with this, consult at least a second opinion of a knowledgeable person.

Subgroup analyses involve splitting all the participant data into subgroups, often so as to make comparisons between them. Subgroup analyses may be done for subsets of participants (such as males and females), or for subsets of studies (such as different geographical locations). Subgroup analyses may be done as a means of investigating heterogeneous results, or to answer specific questions about particular patient groups, types of intervention or types of study. Findings from multiple subgroup analyses may be misleading. Subgroup analyses are observational by nature and are not based on randomized comparisons (an exception is when randomisation is stratified within these subgroups). False negative and false positive significance tests increase in likelihood rapidly as more subgroup analyses are performed (this is due to the multiple testing problem: if you perform a significant test frequently enough, you are likely to find by chance a statistically significant result). If findings are presented as definitive conclusions, there is clearly a risk of patients being denied an effective intervention or treated with an ineffective (or even harmful) intervention. Subgroup analyses can also generate misleading recommendations about directions for future research that, if followed, would waste scarce resources.