5.5.2. Application and examples

The concrete application of these rules differs according to the situation.  Note that imprecision is judged on all outcomes that are judged critical, so the precision of the estimations of the effects on both harms and benefits need to be evaluated.

• Studies indicate a benefit compared to the alternative so you consider recommending the intervention based on the fact that it is beneficial in a clinically significant way.

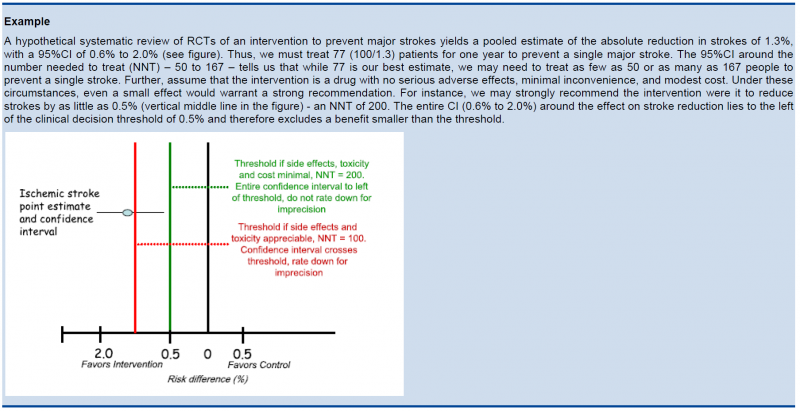
In this case you must prove not only that the pooled or best estimate of the effect is different from no effect but that it is better than the clinical decision threshold.  So the confidence interval must exclude this threshold.

• Studies indicate a harm compared to the alternative so you consider not recommending the intervention based on the fact that it is harmful in a clinically significant way.

In this case you must prove not only that the pooled or best estimate of the effect is different from no effect but that it is more harmful then the clinical decision threshold.  So the confidence interval must exclude this threshold.

• Studies indicate that it is not better than the alternative so you consider not recommending the intervention based on the fact that it is not better in a clinically significant way.

In this case you must prove that the pooled or best estimate of the effect  is lower that the clinical decision threshold.  So the confidence interval must exclude this threshold.

• Studies indicate that it is not more harmful than the alternative so you consider recommending the intervention based on the fact that it is not more harmful in a clinically significant way.

In this case you must prove that the pooled or best estimate of the effect  is lower that the clinical decision threshold.  So the confidence interval must exclude this threshold.

The last two situations amount to proving non superiority or non inferiority. If the line of no effect is crossed, this does not play a major role in the decision.